En géométrie euclidienne, l’aire d’un triangle est une mesure de la surface plane déterminée par trois points et les segments unissant ces points. L’intérêt de l’aire d’un triangle résulte du fait que tout polygone peut être scindé en triangles. Calculer l’aire, c’est indiquer sa surface. Pour un bon résultat, il faut utiliser des formules adaptées. Guide entreprise vous donne toutes les réponses.
Quelles sont les formules basiques des triangles ordinaires ?
Pour calculer l’aire d’un triangle, il suffit de multiplier la base de ce triangle par sa hauteur, et de diviser par deux. La base du triangle est un côté du triangle que l’on choisit.
Le triangle rectangle
Le triangle rectangle a pour propriété de détenir un angle droit, c’est-à-dire un angle à 90°. Le triangle en général est une figure géométrique un peu à part, car tous les autres polygones peuvent eux-mêmes se diviser en triangles de divers types.
La particularité du triangle rectangle, c’est que sa formule de calcul de l’aire peut également s’appliquer aux triangles quelconques, isocèles et équilatéraux. Ceux-ci peuvent aussi être divisés en deux triangles rectangles. On l’appelle ainsi, car il représente exactement la moitié d’un rectangle. Encore une autre façon de calculer son aire.
Pour calculer l’aire d’un triangle rectangle de façon rapide, voici la formule simple :
Aire = (base x hauteur) / 2
Il faut remarquer que le triangle rectangle peut aussi être exposé avec la base sur le dessus, car tout dépend de l’angle droit. Cette formule ressemble beaucoup à celle du calcul de l’aire d’un rectangle (l’aire d’un rectangle étant indiquée par base multiplié par la hauteur). Et comme il a été dit précédemment que le triangle rectangle représente exactement la moitié d’un rectangle. C’est donc la même opération que pour l’aire d’un rectangle, puis il doit être divisé par deux.
Le triangle isocèle
Un triangle isocèle se divise en plusieurs catégories définies par ses angles ou par la longueur. A l’inverse du triangle rectangle, il ne possède pas d’angle droit. D’ailleurs, s’il en possédait un, il deviendrait alors un triangle rectangle. En géométrie, c’est une forme qui détient au préalable deux côtés de même longueur ainsi qu’un axe de symétrie.
La surface d’un triangle isocèle est égale au produit de la longueur de la base par la longueur de la hauteur (issue de la base). Il faut retenir que les longueurs doivent être exprimées dans la même unité de longueur. En plus simple, sa formule est : Aire = Base x Hauteur divisé par deux.
Le triangle équilatéral
Un triangle équilatéral, en géométrie euclidienne, est un triangle dont les trois côtés ont la même longueur. Ses trois angles internes ont la même mesure de 60 degrés, et il constitue ainsi un polygone régulier à trois sommets.
Tous les triangles équilatéraux sont semblables et sont invariants par trois symétries axiales et deux rotations. Le centre est à la fois le centre de gravité, l’orthocentre et le centre des cercles inscrit et circonscrit au triangle. La formule aire d’un triangle équilatéral est la suivante : multiplier la base (la longueur d’un côté) par la hauteur (selon l’axe de symétrie tracé) et diviser le tout par deux.
Comment procéder aux calculs des autres triangles ?
Le triangle scalène
Le triangle scalène est une figure géométrique à trois côtés, dont chacun mesure une longueur distincte. Ce type de polygone est un cas particulier au sein des types de triangle selon la longueur de ses côtés.
Il faut rappeler qu’un polygone est une figure géométrique à deux dimensions qui est formée de l’union de différents points (qui ne font pas partie d’une même ligne) par des segments de ligne. De cette façon, un espace clos est bâti. Un autre point à prendre en compte est que ce type de triangle serait observé comme l’opposé d’un polygone régulier, qui est celui dont les côtés ont la même dimension. Par conséquent, la surface d’un triangle scalène est la moitié de la base multipliée par la hauteur du triangle.
Le triangle obtusangle
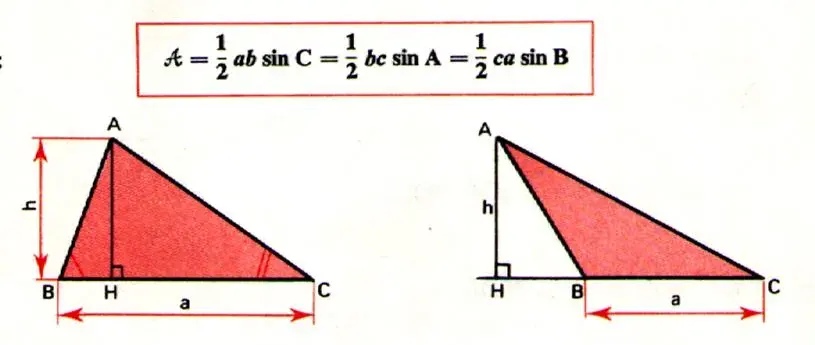
Un triangle obtusangle détient un angle obtus et deux angles aigus. Dans le procédé de calcul de cette figure, la géométrie euclidienne parle d’une somme des mesures des angles intérieurs et d’un triangle étant toujours égale à 180°. En effet, un triangle ne peut avoir plus d’un angle obtus. Il est donc toujours soit obtusangle, soit acutangle, soit rectangle. Un triangle obtusangle (ou aussi amblygone, ou plus simplement obtus) est un triangle qui a un angle obtus. Il est donc le contraire du triangle acutangle qui ne comporte que des angles aigus, et s’oppose aussi au triangle rectangle par l’angle droit de ce dernier et les deux autres aigus.
Par opposition au triangle acutangle, pour un triangle obtusangle, le centre du cercle circonscrit et l’orthocentre sont à l’extérieur du triangle. Il est essentiel de faire la distinction entre ces triangles. En effet, les théorèmes s’appliquent différemment selon les types de triangle.
Il est dit obtusangle s’il possède un angle est supérieur à 90° et les deux autres sont inférieurs à 90°. Pour calculer son aire, sa formule est Aire = (Base × hauteur) / 2 soit : A = (B × h) / 2
Le triangle acutangle
Un triangle acutangle est un trigone muni de trois angles aigus (inférieurs à 90°). Dans certains cas, un triangle peut correspondre à plusieurs catégories. On le nommera alors selon ses différentes caractéristiques.
Géométriquement, la somme des mesures des angles intérieurs d’un triangle étant toujours égale à 180°, un triangle ne peut avoir que zéro ou un angle obtus. Un triangle est donc toujours soit obtusangle, soit acutangle ou droit. Cette différenciation entre les triangles est notamment importante, car certains théorèmes ne s’apposent qu’à un seul modèle de triangles, ou s’appliquent autrement selon le type concerné.
Contradictoirement au triangle obtusangle, pour un triangle acutangle, le centre du cercle circonscrit et l’orthocentre sont à l’interne du triangle. D’où, si b est la longueur d’un côté d’un triangle et h celle de la hauteur relative à ce côté, alors l’aire du triangle est A = 1/2 b x h.

Commentaires récents